234树
234树的节点有三种情况:
1个val值 2个节点(和普通二叉树一致) 2个val值 3个节点 3个val值 4个节点
当节点数超过4时,会发生“节点上溢”现象,上溢后就可以继续插入新元素啦。
B树
B树(B-tree)是一个一般化的二叉查找树(binary search tree),是一种自平衡的树,能够保持数据有序。B树可以拥有多于2个子节点。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在O(logN)时间内完成。
B-树,即为B树。因为B树的原英文名称为B树,而国内很多人喜欢把B树译作B-树,其实,这是个非常不好的直译,很容易让人产生误解。如人们可能会以为B-树是一种树,而B树又是一种树。而事实上是,B-树就是指的B树。
B+树
B+树的B+树元素自底向上插入,这与二叉树恰好相反。
B+树是B树的一种变形形式,B+树上的叶子结点存储关键字以及相应记录的地址,叶子结点以上各层作为索引使用。其特点是能够保持数据稳定有序,其插入与修改拥有较稳定的时间复杂度,和B树一样为O(logN)。一棵 m 阶的B+树定义如下:
- 每个结点至多有 m 个子节点;
- 除根结点外,每个节点至少有 m / 2 个子节点,根结点至少有两个子节点;
- 有k个子节点的节点必有k个关键字。
B+树的查找与B树不同,当索引部分某个结点的关键字与所查的关键字相等时并不停止查找,应继续沿着这个关键字左边的指针向下,一直查到该关键字所在的叶子结点为止。
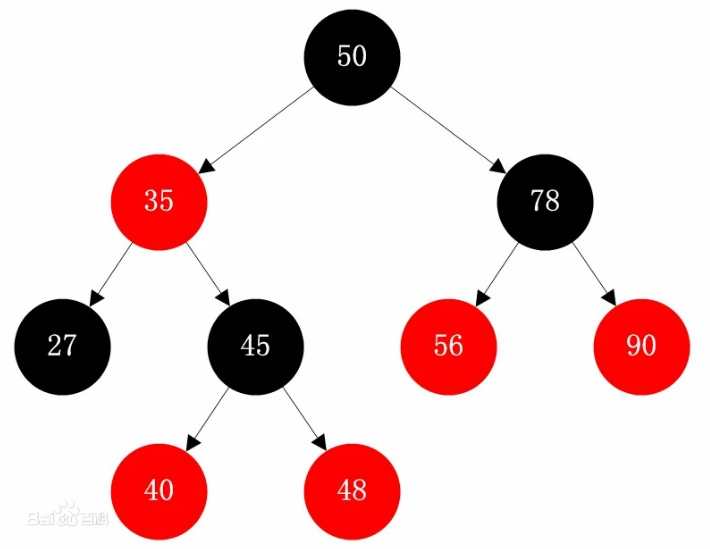
红黑树
红黑树是一种自平衡二叉查找树,典型的用途是实现关联数组。红黑树是在1972年发明,当时被称为平衡二叉B树(symmetric binary B-trees)。后来被修改为如今的“红黑树”。 红黑树是一种特化的AVL树(平衡二叉树),都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。 它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(logN)时间内做查找,插入和删除,这里的 N 是树中元素的数目。
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。 在二叉查找树一般要求以外,红黑树的额外要求如下:
性质1. 节点是红色或黑色。
性质2. 根节点必须是黑色。
性质3. 所有叶子节点都是黑色。
性质4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。